Human body dimensions are frequently stated as percentiles (relative cumulative frequency within a group). Percentiles state, for a given body dimension, the percentage of persons within a random sample who are equal to or smaller than the stated percentile value. Percentiles indicate the highest measured value attained by a defined percentage of the participants in a study.
For example, if the value for the 5th percentile of the body height of men is stated as 1,650 mm, 5% of the subjects studied are 1,650 mm tall or are shorter than 1,650 mm. Conversely, 95% are taller than this figure.
Principle of formation of percentiles, with reference to the example of body height (Schüler 2012). The values measured, for example for the body height, yield the distribution of the individual values of a body dimension. Where the distribution is normal, the highest incidence lies in the middle of the distribution curve (median). In such cases, the following approximation can be made:
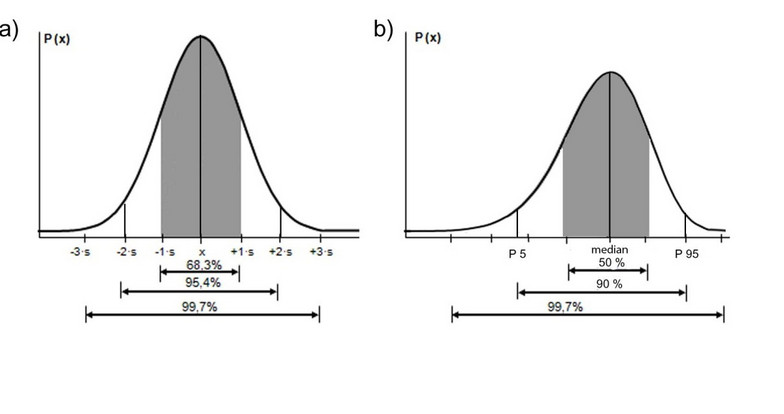
Incidence of body dimensions in percent for (a) Gaussian normal distribution and (b) non-normal distribution (Schüler 2012) Where the distribution is normal, the median (the value of the 50th percentile) is identical to the arithmetic mean. Statement of the standard deviation is then sufficient. This applies in numerous studies to length dimensions (body height, height sitting (trunk length + head height), leg length, etc.) In such cases, the body dimensions within a population can be assumed to be distributed normally. By contrast, circumferential dimensions (waist girth, hip girth, etc.) or breadth dimensions (body breadth sitting) are frequently not distributed normally. In such cases, the use of percentiles is necessary. Percentiles often cannot be calculated from other statistical values.